Khan Academy on a Stick : Matrices

Khan Academy on a Stick

Álgebra

Operaciones de matrices básicas

El mundo virtual de Keany Reeves en "Matrix" (creo que todas las películas juntas se llaman "Las matrices"), tienen que ver con este tutorial más de lo que tal vez sospeches. Las matrices son formas de organizar números. Son usadas ampliamente en los gráficos de computadoras, simulaciones y procesamiento de información en general. Las super inteligencias artificiales que crearon Matrix deben haber usado muchas matrices en el proceso de creación. Este tutorial te introduce a lo que es una matriz y cómo se definen algunas operaciones básicas con ellas.

Multiplicación de una matriz por un vector columna (EN)
Multiplicando una matriz por otra (EN)
Operaciones definidas e indefinidas en matrices (EN)
Multiplicación de matrices (parte 1) (EN)
cc

Multiplicador de matrices de 2 x 2.
Multiplicación de matrices (parte 2) (EN)
cc

Más sobre la multiplicación de matrices.

Multiplicación de matrices

Sabes lo que es una matriz, cómo sumarlas y multiplicarlas por un valor escalar. Ahora definiremos la multiplicación de una matriz por otra. El proceso puede parecer extraño al principio (incluso tal vez un poco después del principio), pero hay cierta naturalidad en el proceso. Cuando estudias álgebra lineal más avanzada y ciencias de la computación, tiene toneladas de aplicaciones (gráficos de computadoras, simulaciones, etc.)

Encontrando el determinante de una matriz de 2 x 2 (ES)
Pista para encontrar el determinante de una matriz de 2 x 2
Inversa de una matriz de 2x2 (EN)
Ejemplo del cálculo de la inversa de una matriz de 2 x 2
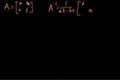La Idea Detrás de la Inversión de una Matriz de 2 x 2 (ES)
cc

¿Cuál es la inversa de una matriz? Ejemplos de inversión de matrices de 2x2.
Matrices para resolver un sistema de ecuaciones (ES)
cc

Usando la inversa de una matriz para resolver un sistema de ecuaciones.
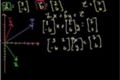Matrices para resolver un problema de combinación de vectores (ES)
cc

Usando matrices para averiguar si alguna combinación de 2 vectores puede crear un tercer vector
Encontrando el determinante de una matriz de 3x3, método 1 (ES)
Encontrando el determinante de una matriz de 3x3, método 2 (ES)
Invirtiendo 3 x 3 parte 1: calcular la matriz de menores y la matriz de Cofactores (ES)
Iniciando nuestro reto para invertir una matriz 3x3. Calculamos la matriz de menores y la matriz de cofactores.
Invertiendo 3 x 3 parte 2: determinante y matriz adjunta (ES)
Terminando nuestra inversión de matriz 3 x 3
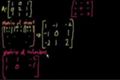Video clásico de la inversión de una matriz de 3x3 parte 1 (ES)
cc

Invirtiendo una matriz de 3x3
Video clásico de la inversión de una matriz de 3x3 parte 2 (ES)
cc

Utilizando la eliminación de Gauss-Jordan para invertir una matriz de 3x3
Matrices Singulares (ES)
cc

Cuándo y por qué no invertir una matriz.

Invirtiendo matrices

Multiplicando por la inversa de una matriz es lo más cercano que tenemos a dividir una matriz. Como multiplicar un número regular por su recíproco para obtener 1, multiplicar una matriz por su inversa nos da la identidad de esa matriz (1 podría ser pensado como la "identidad escalar"). Este tutorial nos llevará a través de este proceso que se convertirá extrañamente en divertido una vez que le agarres el modo.

Matrices: Forma Reducida 1 (ES)
cc

Resolviendo un sistema de ecuaciones lineales haciendo la matriz reducida en su forma reducida
Matrices: Reducida de la forma escalonada en filas 2 (ES)
cc

Otro ejemplo de resolver un sistema lineal de ecuaciones poniendo un matriz aumentada dentro de una forma escalonada por filas
Matrices: Reducida de la forma escalonada en filas 3 (ES)
cc

Y otro ejemplo de solución de un sistema de ecuaciones por medio de tomar la forma reducida de la matriz aumentada

Matriz escalonada reducida por filas

Probablemente ya hayas apreciado que hay varias formas de resolver un sistema de ecuaciones. Bueno, te presentaremos otra forma en este tutorial. Con la forma de una matriz escalonada podemos realizar operaciones con matrices para darles una forma que nos ayude a resolver el sistema.